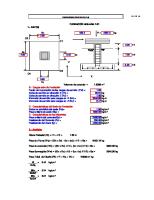
viga fundacion elastica
VIGA SOBRE FUNDACION ELASTICA Consideremos una viga de largo infinito apoyada sobre todo su largo sobre una fundación el
Views 143 Downloads 3 File size 181KB
Recommend stories
- Author / Uploaded
- Jiménez Jorge
Citation preview
VIGA SOBRE FUNDACION ELASTICA Consideremos una viga de largo infinito apoyada sobre todo su largo sobre una fundación elástica. Se aplica una carga puntual P en el origen de los ejes x,y,z. La carga provoca que la viga se deflecte, lo que a su vez desplaza la fundación elástica. Como resultado, una fuerza distribuida se desarrolla entre la viga y la fundación. Por lo tanto, relativa a la viga, la rigidez de la fundación produce una fuerza uniformemente distribuida q en la viga. Para esta deducción, la fuerza q se toma positiva cuando actúa hacia arriba. Cuando la deflexión de la viga es hacia abajo (positiva), el suelo es comprimido y empuja hacia arriba la viga (q positivo). Cuando la deflexión es hacia arriba (negativa), se produce tensión en el suelo.
RSM/2009
1
Consideremos el diagrama de cuerpo libre de un elemento de viga delimitado por dos secciones transversales distanciadas en ∆z. Para el convenio de signos indicado, y pequeños desplazamientos se obtienen las siguientes relaciones diferenciales:
Para una fundación elástica lineal, la carga distribuida q es proporcional a la deflexión de la viga: q =k y Donde el coeficiente de resorte k puede escribirse como: k= b k0 En que b es el ancho uniforme de la viga y k0 es el módulo de la fundación (Westergaard's modulus) cuyas dimensiones son [F/L3]. Cuando la viga descansa sobre una capa de suelo, el módulo de la fundación puede ser altamente variable. A menudo en diseño de fundaciones de edificios, las estimaciones iniciales del módulo k0 se basan en descripciones cualitativas del suelo o algún conocimiento de la resistencia a compresión no confinada qu. Valores de módulo de suelo para arenas y arcillas Tipo de suelo
Rango de k0 [N/mm3]
Arena suelta
0.005 – 0.016
Arena media
0.010 – 0.080
Arena densa
0.063 – 0.126
Arena arcillosa (media)
0.031 – 0.080
Arena limosa (media)
0.024 – 0.048
Arcilla, qu < 0.2 N/mm2
0.012 – 0.024
Arcilla, 0.2 N/mm2 0.4 N/mm2
> 0.048
2
La ecuación diferencial de la viga sobre fundación elástica está dada por:
(2)
(3)
Definiendo
La solución general puede expresarse como:
(4) Esta ecuación representa la solución general para la respuesta de una viga de largo infinito sobre una fundación elástica sometida a una carga puntual. Las constantes se determinan por las condiciones de borde. Como las deflexión tiende a cero para valores grandes de z, las constantes C1 y C2 son cero, y la ecuación anterior se reduce a:
(5) Para determinar las dos constantes en el caso de una viga con carga puntual, usamos las siguientes condiciones: a) la pendiente de la viga es cero bajo la carga debido a la simetría; b) la mitad de la carga P debe ser soportada por la fundación elástica bajo la mitad de la longitud de la viga, especificada por valores positivos de z. Se obtienen las relaciones: en
(6)
y
La condición de pendiente cero en z=0 en ecuación (5) implica C3=C4=C, por lo que la ec. (5) queda como:
(7)
Sustituyendo (7) en (6) se obtiene:
(8)
La ecuación para la deflexión de la viga queda como:
(9) Esta ecuación es válida para valores positivos de z. para valores negativos, por simetría, y(-z)=y(z). La pendiente, momento y corte se obtienen reemplazando ec. (9) en (1).
Como podemos aplicar lo que ya sabemos de métodos energéticos y elementos finitos en el análisis de este tipo de problemas? Para ello derivaremos, a través del principio de Energía Potencial Mínima una matriz de rigidez para una viga apoyada sobre un medio elástico, la cual será luego implementada en una rutina de análisis de vigas y marcos, y estudiaremos la convergencia a la solución teórica. y, v E, I, A mi , θi
mj , θj
Vi
Vj
x, u
k [N/mm2] El funcional de energía potencial se puede escribir como: L 1L 1 L 2 2 π = ∫ EI (v' ' ) dx + axial + k ∫ v dx − ∫ fvdx 20 2 0 0
Notar que aparece un término extra, el cual viene del trabajo hecho por la fundación elástica sobre la viga deflectada. Si k es el coeficiente de rigidez del suelo o fundación, la fuerza restituyente del suelo sobre un elemento diferencial de viga de largo dx es: F = kdx ⋅ v = kvdx El trabajo hecho por esta fuerza es: W = 1 kvdx ⋅ v = 1 kv 2 dx
2
2
Asumiendo que EI es constante a través del largo del elemento, e ignorando los términos axiales, ya que en un análisis lineal su contribución queda desacoplada de los términos del flexión, se tiene: 5
L
L
L
δπ = EI ∫ V' ' δV' ' dx + k ∫ VδVdx − ∫ fδVdx 0
0
V ( x ) = [0 N 1
⇒
N2
0
0 N3
U1 V 1 θ N 4 ] 1 U 2 V2 θ 2
L
V ' ' = N' ' U δV = N δU
δV' ' = N' ' δU
L
L
δπ = EI ∫ ( N' ' U)( N' ' δU)dx + k ∫ ( NU)( NδU)dx − ∫ fNδUdx 0
;
⇒
0
L
0
L
L
δπ = EI ∫ δU N' ' N ' ' Udx + k ∫ δU N NUdx − ∫ fNδUdx T
T
0
T
T
0
0
L T δπ = EIδU ∫ N ' ' N ' ' dx U + kδU T 1 0 4 4244 3 T
K debido a flexion
L L T ∫0 N Ndx U − ∫0 fNδUdx 14243 K debido a fundacion elastica
K = K debido a flexion + K debido a fundacion elastica RSM/2009
6
Utilizando los polinomios de interpolación de Hermite, el primer término de esta ecuación corresponde a la matriz de rigidez regular:
K debido a flexion
EA 0 0 L 12 EI 6 EI 0 L3 L2 6 EI 4 EI 0 L2 L = EA 0 0 − L 12 EI 6 EI 0 − 3 − 2 L L 6 EI 2 EI 0 L2 L
−
EA L 0 0
EA L 0 0
0 12 EI 6 EI − 3 L L2 6 EI 2 EI − 2 L L 0 0 12 EI 6 EI − 2 L3 L 6 EI 4 EI − 2 L L 0
El segundo término, luego de desarrollar las integrales, queda como:
K debido a fundacion elastica
0 0 0 0 0 0 2 13L 11L 9L 13L2 0 − 0 35 210 70 420 11L2 L3 13L2 L3 0 0 − 210 105 420 140 = k 0 0 0 0 0 0 13L 11L2 9L 13L2 0 − 0 210 70 420 35 2 3 2 L 11L L3 13L 0 − − 0 − 420 140 210 105 RSM/2009
7
Se puede implementar esta matriz en una rutina de análisis de marcos planos. Por ejemplo, para los siguientes valores numéricos: P=100000; k=5000; E=29000000; I=100; L=480 in (largo total) =0.02562288 En el centro, para x=0, la solución teórica para deflexión y momento dan: v= 0.2562288 in M=975690.34 lb-in Dividiendo la viga en dos elementos se obtiene: Momento en el centro: M= 1378948 lb-in
El error en la estimación de la deflexión máxima es de un 70.1%, y de 29.2 % en el cálculo del momento.???? Muy mala solucion. Es necesario discretizar más el modelo de elementos finitos.
RSM/2009
8
9
RSM/2009
10